Nature Sleuthing Resumes ….. Sunflowers and Fibonacci; Natural Spirals

November 26, 2023

After a well deserved rest from Inktober and from my self-imposed pressure to create something every day from a list of random prompts, I’m happy to be out again nature sleuthing. Curiosities in nature sometimes stare us in the face. But more often than not making discoveries require keen observational skills, noticing something new to you, and an ability to look for clues to a mystery with wide open eyes.  

It was during a hike on an unseasonably warm day that I paused to admire the dried flower heads from one of the late blooming sunflowers. Have you ever noticed how they look like another kind of sunflower? Papery textured “petals” circle a central disk where a few weeks ago it was crammed full of puffy parachute-topped seeds. After the seeds become airborne, all that’s usually left is a slicked off surface punctuated with dots arranged in spirals radiating out from the center.

Click the link below to read more ………

A Little Botany 101

The anatomy of flowers in the aster (sunflower; daisy) family, Asteraceae, is fascinating. What appears at a glance to be a single flower, is in fact a collection of many small florets. It’s common for many species to display both ray (the outside ring) and disk (the center) florets. However, some species may only have ray florets; some may only have disk florets. 

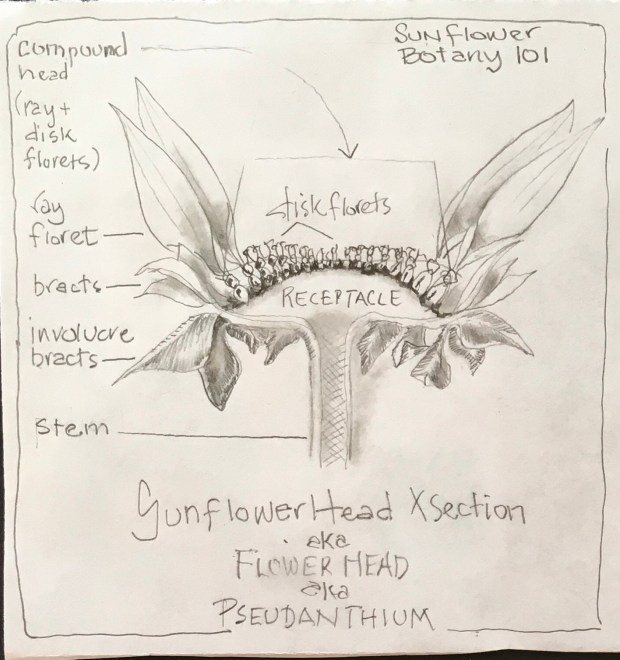
Floret Foundation

All of the florets are supported on a structure called the Receptacle. A spongy layer of material, typically growing in the shape of a disk, the Receptacle often flexes in shape from convex to flat to concave, depending on the stage of floret maturity.  Underneath the Receptacle is a protective ring of leaf-shaped bracts called the Involucre, which can be down- or up-curved, fleshy or stiff and papery, depending on stage of floret maturity. This had me wondering if it was possible to identify a species by its Receptacle shape and Involucre characteristics? Hmmmmmm??????? 

Dried Sunflowers

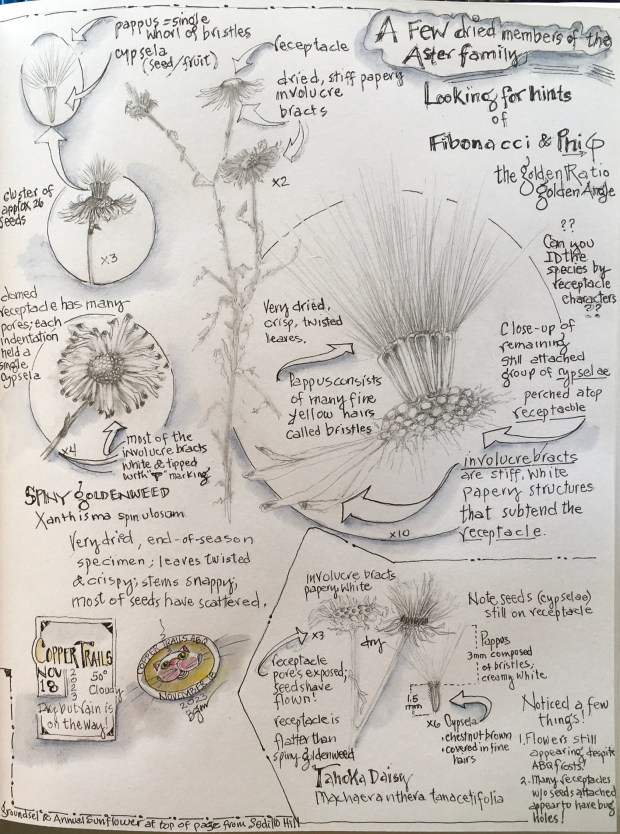
When you hold a dried sunflower head, the “petals” you see are the dried Involucre bracts that surround the naked Receptacle disk. Look closer and notice the Receptacle disk is covered with dots that form a spiral pattern. And look closer still to see the dots spiral clockwise, counterwise and diagonally. Development of the clockwise and counterclockwise spirals is based upon the Fibonacci Sequence. Now I had to learn more!

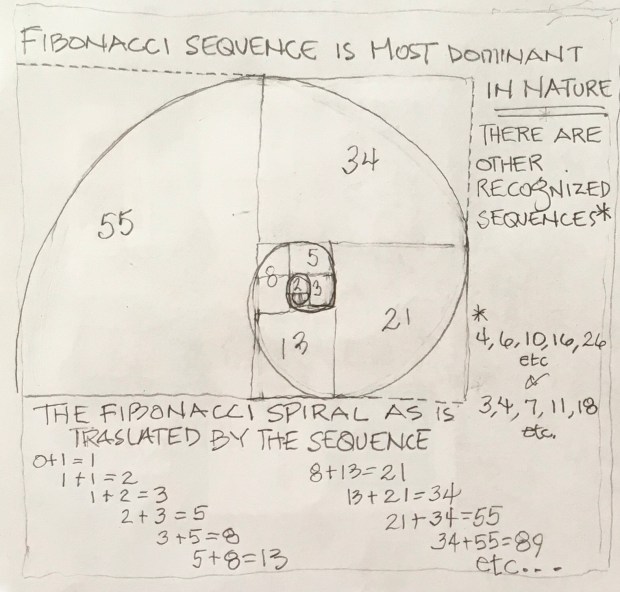
Fibonacci who?

The Fibonacci Sequence was named after the 13th century Italian mathematician, Leonardo of Pisa, better known as Fibonacci. The Sequence itself is easy to understand. Each number in the sequence is derived from the sum of the two preceding numbers. For example:

0+1= 1, 1+1= 2, 1+2= 3, 2+3= 5, 3+5= 8, 5+8= 13, 8+13= 21, 13+21= 34, 21+34= 55, 34+55= 89, 55+89= 144, 89+144= 233 ……….. etc.

Now bring your attention back to that dried sunflower head you’re holding. If you count 5 spirals going in one direction on the surface of the Receptacle, then there will be 8 spirals going in the other direction. This is because 5 and 8 in the Fibonacci Sequence appear back to back. If you count 34 spirals in one direction, there will be 55 spirals going the other way. Again, 34 and 55 are back-to-back in the Sequence. Try it! It works! Larger diameter sunflower heads have higher Sequence numbers (or a larger number of spirals like 89 and 144). Pine cones are another object in nature clearly displaying the Fibonacci Sequence, 8 and 13 (back-to-back Sequence numbers). This is not a coincidence!

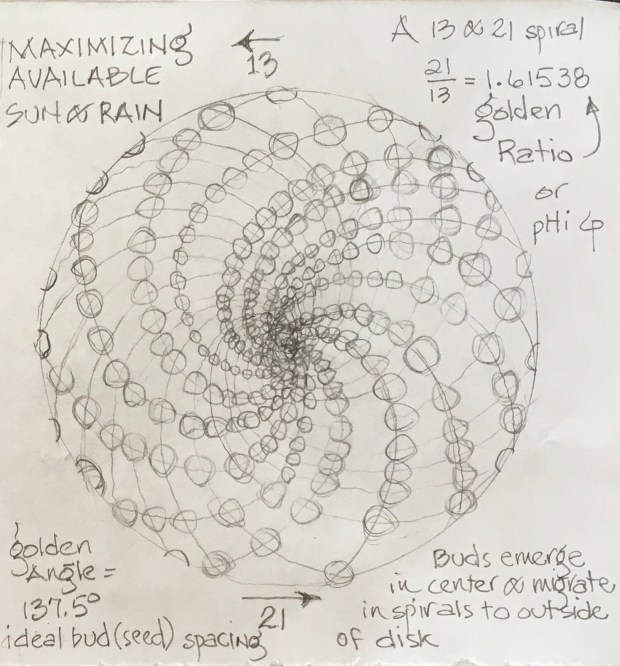
The Receptacle of a sunflower has only limited space to grow and support the next generation of sunflowers, and to be successful as a plant family (Asteraceae), its floret buds and ultimately its seeds must develop as far away as possible from neighboring buds (seeds). This permits the most efficient use of limited space while ensuring the maximum amount of sun and rain are available for each individually developing floret. Wow! I always knew sunflowers were wise! But wait! Just how far apart are these florets? 

Enter the Golden Angle and the Golden Ratio!

Studies have shown that in order to maximize light and water availability for each developing sunflower bud, the distance apart is based on an angle of 137.5 degrees away from the bud(s) that came before. The Golden Angle is 137.5 degrees!  But before taking this leap, know that the Golden Angle is famous for being derived from a number called the Golden Ratio, which happens to be the irregular number,1.618033………, which like Pi goes on forever. So the larger the back-to-back Fibonacci Sequence numbers are, the closer to the Golden Ratio of 1.618033 you get. The largest sunflowers are the most efficient in maximizing the sun and rain available to each bud, flower, and seed. See for yourself …..

8/13=1.625, 13/21=1.61538, 21/34=1.619047, ………. 144/89=1.61797, 233/144=1.618055

A Pause to Wonder Outloud!
So is it possible to ever become the most efficient sunflower seed generator ever? How many spirals would be needed to achieve this goal, if it is achievable? Since the Golden Ratio is an irregular number (never ending), perhaps it’s not possible, but it would be cool to know how close it could get before undeveloped buds and/or seeds began spilling out of the sunflower head! If the Golden Ratio is irregular, maybe there’s no limit to the size to which a sunflower head can grow? Who, if anyone, knows these things? Would this be important somehow (unlimited quantities of sunflower seeds to feed the world or at least all of the birds in the world)? Does Carrying Capacity enter into this possibility like it does with animal populations? Thoughts for another day.

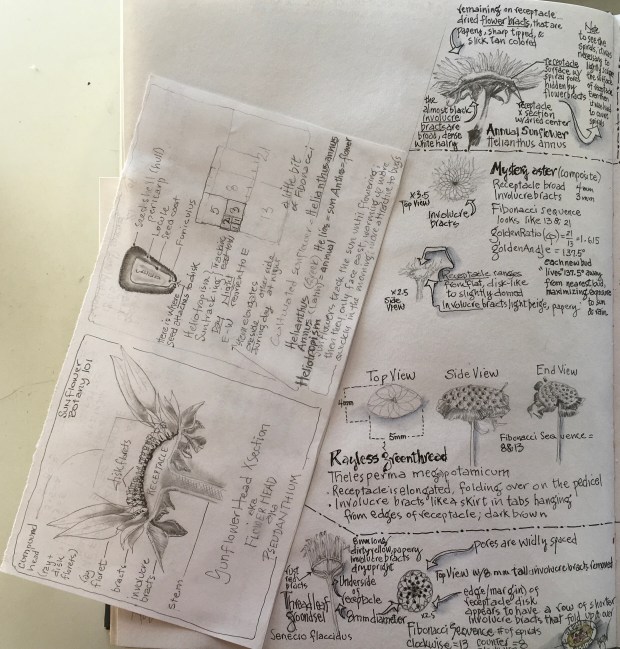
Today, I’m merely wondering if each species in the family Asteraceae has its own constant number of Receptacle disk spirals (which, by the way = the Seed Head), along with other characteristics that are species specific? And can you identify a species by counting spirals and Receptacle disk size, shape, color, and/or depth of disk dots?! 

Right now, all I know is my minuscule collection of dried Receptacle disks showed distinct differences between species. 

If you’ve come this far, you are indeed a geek in good company! Congratulations and Thank You. Oh, and I’d love to hear your thoughts (about anything)!